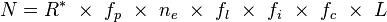TEORÍA DEL CAOS.
Caos. Cuando oyes esta palabra, puedes pensar en tu habitación, o en el examen de física de la semana que viene. Pero aquí vamos a tratar la teoría del caos, y si tratamos la teoría del caos, tenemos necesariamente que tratar el efecto mariposa, ya que están relacionados, de manera muy estrecha.
La teoría del caos es una rama de las matemáticas y la física, que se ve influida mucho por las pequeñas variaciones. Una variación que, para nosotros sea insignificante, puede influir de manera trascendental en nuestra vida.
Un claro ejemplo de una rama que se vea afectada por la teoría del caos es la meteorología. Esto lo comprobó el meteorólogo Edward Lorenz.
Supongamos que tenemos un programa de ordenador, capaz de resolver una ecuación, de forma que cuando introducimos un valor, al que podemos llamar x, al cabo de un tiempo (t), nos da un resultado. El resultado puede ser la presión atmosférica en una zona determinada, las posibilidades de que un volcán erupcione o cualquier otra cosa.
Introducimos un valor x=3,4567. Al cabo de un segundo, este valor, por medio de la ecuación, se convierte en 130. Al cabo de una semana, este valor pasa a ser 300.
Introduzcamos ahora el valor 3,456. Es un valor que no varía mucho del inicial. Al cabo de un segundo, obtenemos nuevamente 130, y al cabo de una semana, 299,24.
Nos puede parecer que es error es bastante normal, ya que nos varía 76 centésimas solamente. Pero lo que estaría fuera de toda previsión sería que nuestro resultado final fuera 839,48. Es decir, que una variación de tan sólo 7 diez milésimas, nos provocara un error tan grande. Esto es lo que sucede en los llamados (con razón) sistemas caóticos, y con lo que Edward Lorenz, matemático puro, que trabajó en la meteorología por puro azar, se encontró con que le ocurría algo parecido a lo que nos pasa en el ejemplo.
Lo que este meteorólogo hizo fue calcular el tiempo previsto introduciendo en un ordenador unos datos bastante buenos, con más de seis decimales. Al calcular el resultado con estos datos, la predicción era de un día soleado para el próximo día.
Sin embargo, Lorenz decidió calcular los datos de nuevo, pero esta vez, para ahorra tiempo, introdujo los datos con solo tres decimales. El resultado era sorprendente: La predicción era de lluvia intensa para el próximo día. Lorenz se quedó asombrado, ya que solo por tres decimales menos, lo que conlleva un error de menos de una milésima, puede cambiar las condiciones meteorológicas de forma tan radical.
Probablemente, el primer matemático que tuvo el caos ante sí fue probablemente Henri Poincaré, al estudiar un sistema gravitatorio de tres cuerpos. Después de Poincaré, Lorenz fue el siguiente en tratar la teoría del caos, aplicándola a la meteorología, y la teorizó, abriendo nuevas investigaciones para los matemáticos de la época. Pero no sólo las matemáticas se ven afectadas por la teoría del caos; también las ciencias de la naturaleza, y en el espacio exterior. Se ha podido rastrear la presencia del caos en fenómenos tan diversos como las franjas vacías de los anillos de asteroides, o en el crecimiento de las poblaciones de insectos, el goteo de un grifo, el metabolismo celular...
También se especula con que el funcionamiento de nuestro cerebro puede no obedecer a un sistema lineal fijo, sino que estaría condicionado por pequeños factores que cambiarían su funcionamiento, o lo que es lo mismo, que estaría bajo la influencia de la teoría del caos. Esta teoría se ha usado con éxito en el diseño de redes de neuronas creadas artificialmente.
EL EFECTO MARIPOSA.
El efecto mariposa, que deriva de la teoría del caos, nos propone que una pequeña acción, que puede no tener consecuencias inmediatas, al cabo de un determinado tiempo puede causar cosas que no podríamos haber imaginado desde un principio.
La frase que ha dado el nombre al efecto mariposa es “El aleteo de una mariposa en Londres puede provocar al mes siguiente una tormenta en Hong Kong.”
Lo que esta frase quiere decir, es que dos hechos separados en el espacio y en el tiempo, pueden estar relacionados entre sí, y que cuando esto se repite, al final acaba apareciendo el patrón.
Un ejemplo claro sobre el efecto mariposa es soltar una pelota justo sobre la arista del tejado de una casa varias veces; pequeñas desviaciones en la posición inicial pueden hacer que la pelota caiga por uno de los lados del tejado o por el otro, conduciendo a trayectorias y posiciones finales completamente diferentes. Cambios minúsculos que conducen a resultados totalmente diferentes.
La teoría del caos también se relaciona con los fractales. Antes de nada, necesitamos saber que es un fractal. Un fractal es una estructura que se repite indefinidamente, por ejemplo, un copo de nieve:
¿Qué relación hay entre los fractales y la teoría del caos? Existe una relación entre ellos en la que se ve implicado el infinito. Se podrían llenar páginas y páginas con el infinito y los fractales, pero no vamos a tratar eso aquí.
Un ejemplo fácil, sería decir que el perímetro, o el área de un fractal son infinitos. Es difícil de entender, pero si nos paramos a mirar cuanto mide el perímetro de, por ejemplo, la curva de Koch, conocido fractal, nos damos cuenta de que, como se repite hasta el infinito, su perímetro, y también su área, son infinitos.
 |
| Curva de Koch |
Atractores: Se podría decir, que un atractor es, de alguna forma, la geometría de la teoría del caos.
En general, existen tres tipos de atractores, los más comunes, que son el punto, la circunferencia, y el toro, una figura con la forma de una rosquilla. Es decir, que las trayectorias de las partículas acaban por adquirir la forma de alguno de estos tres atractores, llamados atractores clásicos. Pero hay algunos sistemas que no presentan la forma de un atractor clásico, sino la de un atractor extraño. ¿Cuál es la diferencia? Un atractor extraño es un fractal. Debido a esto, se les ha empezado a llamar atractores fractales.
El descubrimiento de estos atractores ha producido un gran interés en el mundo científico, ya que los atractores fractales están presentes en muchas cosas alrededor nuestra, como, por poner un ejemplo, el crecimiento de la población del escarabajo de la harina. Dicho crecimiento fue estudiado por un equipo de biólogos en 1997, donde se revelaba que el crecimiento era un factor caótico con un atractor fractal.
Ejemplos de películas en las que aparece la teoría del caos.
Una película en la que aparece la teoría del caos, no es otra que Caos.
Ficha técnica:
Dirección y guión: Tony Giglio.
País: USA.
Año: 2006.
Duración: 98 min.
Género: Thriller, acción.
Interpretación: Jason Statham (Quentin Conners), Ryan Philippe (Shane Dekker), Wesley Snipes (Lorenz), Henry Czerny (Capitán Martin Jenkins), Justine Waddell (Teddy Galloway), Nicholas Lea (Vincent Durano), Jessica Steen (Karen Cross), Rob LaBelle, John Cassini (Bernie Callo), Damon Johnson (Brandon Dax), Paul Perri (Harry Hume).
Producción: Huw Penalt Jones, Gavin Wilding y Michael Derbas.
Música: Trevor Jones.
Fotografía: Richard Greatrex.
Montaje: Sean Barton.
Diseño de producción: Chris August.
Vestuario: Bobbie Read.
Estreno en España: 12 Mayo 2006.
 |
| Quentin Conners y Shane Dekker. |
Sinopsis: Todo comienza una mañana, aparentemente normal, en un banco en la ciudad Estadounidense de Seattle. Cinco hombres, vestidos de negro, y armados, entran en un banco, tomando a todo el mundo como rehenes. La policía llega, y rodean a los atracadores. El cabecilla, Lorenz, pide un negociador y exige que sea el detective Quentin Conners. Conners vuelve a su puesto tras su reciente expulsión causada por un incidente fortuito que terminó con la muerte de un rehén, una joven secuestrada. Su supervisor se ve forzado a readmitir a Conners para el caso, pero le pone a trabajar con un recién llegado de la academia de policía, el novato detective Shane Dekker. Conners contacta con Lorenz y comienza un proceso de negociación. Se organiza una táctica muy precisa de entrada al banco, pero se convierte en una batalla campal y los ladrones consiguen escapar, camuflados entre los rehenes. Los detectives descubren que, aunque no se han llevado nada del banco, han robado, por medio de los ordenadores del banco, más de mil millones de dólares. Empieza así una carrera para detener a los ladrones y recuperar el dinero, y donde también tiene su papel la teoría del Caos.
 |
| Lorenz, contactando con Conners. |
La teoría del caos aparece en algunos diálogos, por ejemplo en el que Shane Dekker pregunta a Conners si conoce la teoría del Caos, ya que Lorenz habla de una manera extraña, como si tratara de decirles algo, empleando mucho la palabra Caos. La frase es: No se puede controlar a todos los rehenes si dejas que una mala acción quede impune. Podrían revelarse al azar. El caos, conlleva cierto orden. A partir de esto, Dekker le habla a Conners de la teoría del Caos.
José Carlos Entrena.
 Si medimos con el transportador cada uno de los ángulos correspondientes a cada vértice y se suman los valores obtenidos, esta suma es aproximadamente 180º.
Si medimos con el transportador cada uno de los ángulos correspondientes a cada vértice y se suman los valores obtenidos, esta suma es aproximadamente 180º.